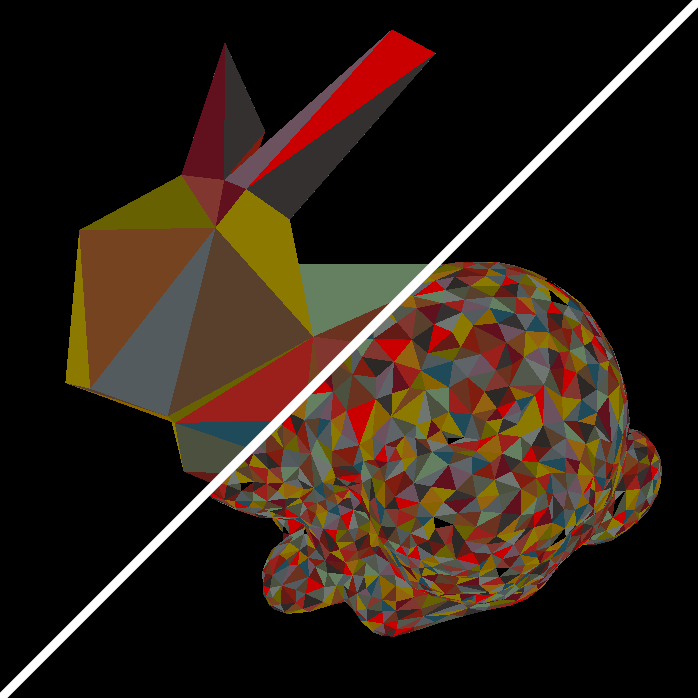Recreating Nanite: LOD generation
Matching commits:
- Support for LODs inside glTF
- First version of LOD clusters
- Small fix in GLTFProcessing when building METIS graph
- Vertex welding & METIS edge weights
- k-d tree usage for simplification (commit message is wrong due to a mistake)
- Recreate k-d tree for each LOD
Summary:
Introduction
I thought LOD generation would take longer than all previously discussed features from this article series. I was right, but it took even longer than expected.
Interestingly, an article about this exact topic was relayed by Jendrik Illner on his website, a few weeks ago: Creating a Directed Acyclic Graph from a Mesh by Traverse Research.
The article goes into details on how Traverse Research creates their LOD based on meshlets. There are a few details different from Unreal’s (or my own) implementation, but the idea is the exact same:
- Split the initial mesh into clusters of X triangles
- Group the clusters based on connectivity
- Simplify each group independently, making sure to lock the borders of the group (to avoid cracks with different LODs).
- Split the simplified group into new clusters
- If you still have more than Y clusters, goto step 2.
This article will describe how I managed to implement my own version, using Meshoptimizer and METIS. I will focus mostly on a few points to keep in mind when implementing your own version, and the mistakes I have made along the way.
Small note: You may notice during this article that meshes are drawn to the final image, contrary to the previous articles. This is because I worked on the material pass before LOD generation in my implementation, but the material pass will be the subject of a future article.
Encoding LODs inside glTF
Before trying to create LODs, I need to first make sure the engine can load them properly.
I decided not to overcomplicate things, meshlets will just have a “LOD” field which are kept until rendering.
struct Meshlet {
std::uint32_t vertexOffset = 0;
std::uint32_t vertexCount = 0;
std::uint32_t indexOffset = 0;
std::uint32_t indexCount = 0;
+ std::uint32_t lod = 0;
};
In the previous article, I have said that I stored meshlets as vectors of 4 unsigned ints (uvec4), because it matched the size of my struct. However, with the addition of this LOD field, the struct no longer fits inside a uvec4, so a few changes on saving and loading are required:
Here’s serialization:
// meshlet data
{
const std::size_t meshletCount = primitive.meshlets.size();
const std::size_t meshletStartIndex = meshletBuffer.data.size();
const std::size_t bufferSize = meshletCount * sizeof(Carrot::Render::Meshlet);
meshletBuffer.data.resize(meshletStartIndex + bufferSize);
memcpy(meshletBuffer.data.data() + meshletStartIndex, primitive.meshlets.data(), bufferSize);
tinygltf::Accessor& accessor = model.accessors.emplace_back();
accessor.bufferView = meshletBufferViewIndex;
accessor.byteOffset = meshletStartIndex;
- accessor.count = meshletCount;
+ accessor.count = bufferSize;
accessor.name = Carrot::sprintf("%s-meshlets", primitive.name.c_str());
- accessor.type = TINYGLTF_TYPE_VEC4;
+ accessor.type = TINYGLTF_TYPE_SCALAR;
- accessor.componentType = TINYGLTF_COMPONENT_TYPE_UNSIGNED_INT;
+ accessor.componentType = TINYGLTF_COMPONENT_TYPE_UNSIGNED_BYTE;
}
Writing meshlets to the meshlet buffer
Note that I now write an array of bytes instead of an array of uvec4, this has a small implication when reading from the glTF.
{
auto& meshletBuffer = model.buffers[meshletBufferIndex];
auto& meshletsBufferView = model.bufferViews[meshletBufferViewIndex];
meshletsBufferView.name = "Meshlets";
meshletsBufferView.byteLength = meshletBuffer.data.size();
meshletsBufferView.byteOffset = 0;
+ meshletsBufferView.byteStride = sizeof(Carrot::Render::Meshlet);
meshletsBufferView.buffer = meshletBufferIndex;
}
Specifying the stride, and deviating from the glTF format
To ensure the data is loaded properly, I need to set the stride. Otherwise, a meshlet would span a single byte.
Here, I had to workaround the glTF specification, because as far I know there is no “binary” data type, only scalar, vectors and matrices.
The “true” glTF way would probably be to specify a different accessor for each of Meshlet’s fields, but I am doing this for my own engine so I want to keep things simple.
If meshlets and/or cluster hierarchies were to get added to glTF as an extension in the future, I would expect different accessors for vertex/index offset/count.
Finally, I need to be able to load the new format:
const tinygltf::Accessor& accessor = model.accessors[meshletsAccessorIndex];
- loadedPrimitive.meshlets.resize(accessor.count);
+ loadedPrimitive.meshlets.resize(accessor.count / sizeof(Carrot::Render::Meshlet));
Carrot::Async::parallelFor(loadedPrimitive.meshlets.size(), [&](std::size_t i) {
loadedPrimitive.meshlets[i] = readFromAccessor<Carrot::Render::Meshlet>(i, accessor, model);
// ...
Loading the new format
The only difference here is that the accessor spans all bytes of meshlet data, instead of counting the number of meshlets. This is because I store the meshlet as an array of unsigned bytes,
which from the point of view of glTF means that I have N x sizeof(Meshlet) elements (where N is the number of meshlets).
LOD generation
First approach
This first approach only works for connected meshes (ie a mesh after welding / merging vertices by distance). It will be refined in the next sections to work on faceted meshes.
Small reminder of what needs to happen to generate a cluster hierarchy:
- Split the initial mesh into clusters of X triangles
- Group the clusters based on connectivity
- Simplify each group independently, making sure to lock the borders of the group (to avoid cracks with different LODs).
- Split the simplified group into new clusters
- If you still have more than Y clusters, goto step 2.
After the previous article, step 1 is already done because the mesh is split into meshlets of maximum 128 triangles.
Therefore I need to draw the rest of the owl implement steps 2 through 5.
Grouping clusters
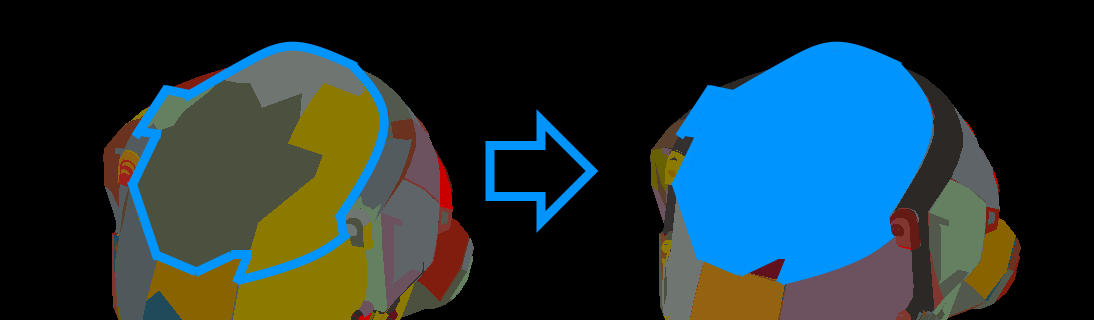
Let’s assume LOD N is already done, and let’s examine how to group clusters for LOD N+1:
Damaged Helmet, upper part of visor is surrounded by blue lines to show limits of a cluster group. Left side is LOD 0, right side is LOD 1
The clusters need to be grouped based on their connectivity, and on their shared boundary. The goal is to create groups which will simplify greatly (connectivity), and avoids locking too many vertices at each step (maximize shared edges).
Therefore, I need to find a grouping of connected clusters, which maximizes the amount of shared edges between clusters. Epic Games and Traverse Research use the METIS library to solve this partitioning problem. I am not going to be original and I will use the exact same solution.
Small note on METIS:
Its CMakeLists.txt on GitHub does not work when loaded as a subdirectory. My fork has a fix for this, but requires GKlib (same author) to be present inside the METIS folder (forgot to add it properly as a submodule). However, I decided to distribute METIS as a static library in my engine, just for convenience.
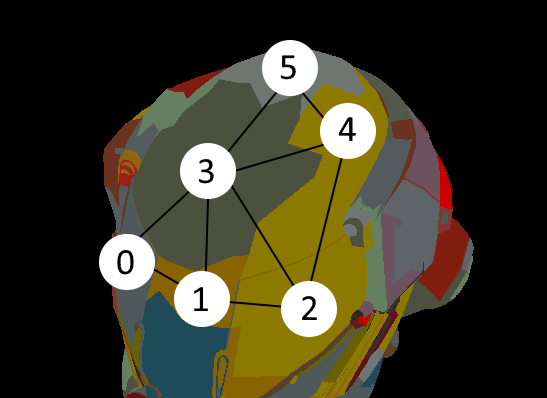
The idea is to represent the clusters as a graph. Clusters are vertices, and edges are connections between clusters. Edge weights will be the number of shared edges between two clusters.
Damaged Helmet, with graph of some connected clusters
Let’s get coding!
groupMeshlets will take a list of meshlets, and output a list of groups. Each group will hold the indices of the meshlets it contains.
I want to group meshlets by groups of 4, so I first need to ensure I can create at least two groups:
struct MeshletGroup {
std::vector<std::size_t> meshlets;
};
static std::vector<MeshletGroup> groupMeshlets(LoadedPrimitive& primitive, std::span<Meshlet> meshlets) {
// ===== Build meshlet connections
auto groupWithAllMeshlets = [&]() {
MeshletGroup group;
for (int i = 0; i < meshlets.size(); ++i) {
group.meshlets.push_back(i);
}
return std::vector { group };
};
if(meshlets.size() < 8) {
return groupWithAllMeshlets();
}
// ...
Then I have to figure out which meshlets are connected.
The idea is to identify edges by the vertex pair (a, b), where a and b are indices inside the vertex buffer, and a < b.
I iterate over all edges of all meshlets, recording their edges each time (meshlets2Edges). At the same time, I store the list of meshlets corresponding to a given edge (edges2Meshlets).
// ...
/**
* Connections betweens meshlets
*/
struct MeshletEdge {
explicit MeshletEdge(std::size_t a, std::size_t b): first(std::min(a, b)), second(std::max(a, b)) {}
bool operator==(const MeshletEdge& other) const = default;
const std::size_t first;
const std::size_t second;
};
struct MeshletEdgeHasher {
std::size_t operator()(const MeshletEdge& edge) const {
std::size_t h = edge.first;
Carrot::hash_combine(h, edge.second);
return h;
}
};
// meshlets represented by their index into 'meshlets'
std::unordered_map<MeshletEdge, std::vector<std::size_t>, MeshletEdgeHasher> edges2Meshlets;
std::unordered_map<std::size_t, std::vector<MeshletEdge>> meshlets2Edges; // probably could be a vector
// for each meshlet
for(std::size_t meshletIndex = 0; meshletIndex < meshlets.size(); meshletIndex++) {
const auto& meshlet = meshlets[meshletIndex];
auto getVertexIndex = [&](std::size_t index) {
return primitive.meshletVertexIndices[primitive.meshletIndices[index + meshlet.indexOffset] + meshlet.vertexOffset];
};
const std::size_t triangleCount = meshlet.indexCount / 3;
// for each triangle of the meshlet
for(std::size_t triangleIndex = 0; triangleIndex < triangleCount; triangleIndex++) {
// for each edge of the triangle
for(std::size_t i = 0; i < 3; i++) {
MeshletEdge edge { getVertexIndex(i + triangleIndex * 3), getVertexIndex(((i+1) % 3) + triangleIndex * 3) };
edges2Meshlets[edge].push_back(meshletIndex);
meshlets2Edges[meshletIndex].emplace_back(edge);
}
}
}
// remove edges which are not connected to 2 different meshlets
std::erase_if(edges2Meshlets, [&](const auto& pair) {
return pair.second.size() <= 1;
});
if(edges2Meshlets.empty()) {
return groupWithAllMeshlets();
}
// at this point, we have basically built a graph of meshlets, in which edges represent which meshlets are connected together
// ...
The last piece of the puzzle is to create the graph for METIS to partition. METIS expects the graph to be represented in “compressed storage format”.
This format is based on 2 arrays: xadj and adjncy.
adjncy is a list of edges, which needs xadj to make sense:
for vertex N, the range xadj[N] to xadj[N+1] (non inclusive) is the range of indices inside adjncy of vertices N is connected to.
Example to iterate over vertices connected to vertex 2:
int vertexA = 2;
for (int adjIndexVertexB = xadj[vertexA]; adjIndexVertexB < xadj[vertexA + 1]; adjIndexVertexB++)
{
int vertexB = adjncy[adjIndexVertexB];
// report pair (a, b)
}
I want an edge-cut, to minimize the cost of separating groups (called partitions in graph theory). Cost between partitions corresponds to the amount of connections between meshlet groups in our case, and that’s what I want to minimize. To put it in other words: I want to group meshlets which are highly connected.
Here’s how I fill this information (and setup METIS):
// ...
// idx_t comes from METIS and corresponds to std::uint64_t in my build of METIS
idx_t vertexCount = meshlets.size(); // vertex count, from the point of view of METIS, where Meshlet = vertex
idx_t ncon = 1; // only one constraint, minimum required by METIS
idx_t nparts = meshlets.size()/4; // groups of 4
verify(nparts > 1, "Must have at least 2 parts in partition for METIS");
idx_t options[METIS_NOPTIONS];
METIS_SetDefaultOptions(options);
// edge-cut, ie minimum cost betweens groups.
options[METIS_OPTION_OBJTYPE] = METIS_OBJTYPE_CUT;
options[METIS_OPTION_CCORDER] = 1; // identify connected components first
// prepare storage for partition data
// each vertex will get its partition index inside this vector after the edge-cut
std::vector<idx_t> partition;
partition.resize(vertexCount);
// xadj
std::vector<idx_t> xadjacency;
xadjacency.reserve(vertexCount + 1);
// adjncy
std::vector<idx_t> edgeAdjacency;
// weight of each edge
std::vector<idx_t> edgeWeights;
for(std::size_t meshletIndex = 0; meshletIndex < meshlets.size(); meshletIndex++) {
std::size_t startIndexInEdgeAdjacency = edgeAdjacency.size();
for(const auto& edge : meshlets2Edges[meshletIndex]) {
auto connectionsIter = edges2Meshlets.find(edge);
if(connectionsIter == edges2Meshlets.end()) {
continue;
}
const auto& connections = connectionsIter->second;
for(const auto& connectedMeshlet : connections) {
if(connectedMeshlet != meshletIndex) {
auto existingEdgeIter = std::find(edgeAdjacency.begin()+startIndexInEdgeAdjacency, edgeAdjacency.end(), connectedMeshlet);
if(existingEdgeIter == edgeAdjacency.end()) {
// first time we see this connection to the other meshlet
edgeAdjacency.emplace_back(connectedMeshlet);
edgeWeights.emplace_back(1);
} else {
// not the first time! increase number of times we encountered this meshlet
std::ptrdiff_t d = std::distance(edgeAdjacency.begin(), existingEdgeIter);
assert(d >= 0);
verify(d < edgeWeights.size(), "edgeWeights and edgeAdjacency do not have the same length?");
edgeWeights[d]++;
}
}
}
}
xadjacency.push_back(startIndexInEdgeAdjacency);
}
xadjacency.push_back(edgeAdjacency.size());
verify(xadjacency.size() == meshlets.size() + 1, "unexpected count of vertices for METIS graph?");
verify(edgeAdjacency.size() == edgeWeights.size(), "edgeWeights and edgeAdjacency must have the same length");
// ...
METIS can easily create segfaults if your storage size is wrong, and they are NOT fun to debug. So triple check your vector sizes!
Finally, I just need to call the proper METIS function, and return the generated groups!
// ...
idx_t edgeCut; // final cost of the cut found by METIS
int result = METIS_PartGraphKway(&vertexCount,
&ncon,
xadjacency.data(),
edgeAdjacency.data(),
nullptr, /* vertex weights */
nullptr, /* vertex size */
edgeWeights.data(),
&nparts,
nullptr,
nullptr,
options,
&edgeCut,
partition.data()
);
verify(result == METIS_OK, "Graph partitioning failed!");
// ===== Group meshlets together
groups.resize(nparts);
for(std::size_t i = 0; i < meshlets.size(); i++) {
idx_t partitionNumber = partition[i];
groups[partitionNumber].meshlets.push_back(i);
}
return groups;
// end of function
Whew, that’s a lot of code! But the rest of the first approach is rather straight forward and short in comparison.
Simplifying cluster groups
Meshlets are now grouped, I need to merge and simplify them.
For each group, I start by creating an index buffer which will be the concatenation of index buffers of its meshlets:
for(const auto& group : groups) {
std::vector<unsigned int> groupVertexIndices;
// add cluster vertices to this group
// and remove clusters from clusters to merge
for(const auto& meshletIndex : group.meshlets) {
const auto& meshlet = primitive.meshlets[meshletIndex];
std::size_t start = groupVertexIndices.size();
groupVertexIndices.resize(start + meshlet.indexCount);
for(std::size_t j = 0; j < meshlet.indexCount; j++) {
groupVertexIndices[j + start] = primitive.meshletVertexIndices[primitive.meshletIndices[meshlet.indexOffset + j] + meshlet.vertexOffset];
}
}
// ...
At this point, groupVertexIndices is an index buffer containing all triangles of the meshlets inside the group.
That has the effect of merging the meshlets into a new “big” meshlet, which I need to simplify:
float targetError = 0.01; // will be modified after
// remove 50% of triangles
const float threshold = 0.5f;
std::size_t targetIndexCount = groupVertexIndices.size() * threshold;
unsigned int options = meshopt_SimplifyLockBorder; // we want all group borders to be locked (because they are shared between groups)
std::vector<unsigned int> simplifiedIndexBuffer;
simplifiedIndexBuffer.resize(groupVertexIndices.size());
float simplificationError = 0.f;
std::size_t simplifiedIndexCount = meshopt_simplify(simplifiedIndexBuffer.data(), // output
groupVertexIndices.data(), groupVertexIndices.size(), // index buffer
&primitive.vertices[0].pos.x, primitive.vertices.size(), sizeof(Carrot::Vertex), // vertex buffer
targetIndexCount, targetError, options, &simplificationError
);
simplifiedIndexBuffer.resize(simplifiedIndexCount);
I need to use meshopt_SimplifyLockBorder to ensure the border of the group are not modified during simplification, to avoid seams.
targetError is used to determine how much deformation is allowed. For now it is set to 1%, but I will modify it later in this article, to allow lower quality LODs to have more error.
After this step, simplifiedIndexBuffer should contain an index buffer representing the result of simplifying the merged meshlets! However, if simplification cannot procede without increasing the error above targetError, the simplified index buffer might be bigger than 50% of the original index buffer. This is a problem I will encounter and try to workaround in a later part of this article.
Splitting cluster groups
Thankfully, as noted in the Nanite presentation, splitting cluster groups and generating the initial meshlets (at LOD 0) are exactly the same problem!
This means I can just reuse the code from the previous article on cluster rendering, and continue from there!
After a tiny refactoring, here’s what it looks like:
static void appendMeshlets(LoadedPrimitive& primitive, std::span<std::uint32_t> indexBuffer) {
constexpr std::size_t maxVertices = 64;
constexpr std::size_t maxTriangles = 128;
const float coneWeight = 0.0f; // for occlusion culling, currently unused
const std::size_t meshletOffset = primitive.meshlets.size();
const std::size_t vertexOffset = primitive.meshletVertexIndices.size();
const std::size_t indexOffset = primitive.meshletIndices.size();
const std::size_t maxMeshlets = meshopt_buildMeshletsBound(indexBuffer.size(), maxVertices, maxTriangles);
std::vector<meshopt_Meshlet> meshoptMeshlets;
meshoptMeshlets.resize(maxMeshlets);
std::vector<unsigned int> meshletVertexIndices;
std::vector<unsigned char> meshletTriangles;
meshletVertexIndices.resize(maxMeshlets * maxVertices);
meshletTriangles.resize(maxMeshlets * maxVertices * 3);
const std::size_t meshletCount = meshopt_buildMeshlets(meshoptMeshlets.data(), meshletVertexIndices.data(), meshletTriangles.data(), // meshlet outputs
indexBuffer.data(), indexBuffer.size(), // original index buffer
&primitive.vertices[0].pos.x, // pointer to position data
primitive.vertices.size(), // vertex count of original mesh
sizeof(Carrot::Vertex), // stride
maxVertices, maxTriangles, coneWeight);
const meshopt_Meshlet& last = meshoptMeshlets[meshletCount - 1];
const std::size_t vertexCount = last.vertex_offset + last.vertex_count;
const std::size_t indexCount = last.triangle_offset + ((last.triangle_count * 3 + 3) & ~3);
primitive.meshletVertexIndices.resize(vertexOffset + vertexCount);
primitive.meshletIndices.resize(indexOffset + indexCount);
primitive.meshlets.resize(meshletOffset + meshletCount); // remove over-allocated meshlets
Carrot::Async::parallelFor(vertexCount, [&](std::size_t index) {
primitive.meshletVertexIndices[vertexOffset + index] = meshletVertexIndices[index];
}, 1024);
Carrot::Async::parallelFor(indexCount, [&](std::size_t index) {
primitive.meshletIndices[indexOffset + index] = meshletTriangles[index];
}, 1024);
// meshlets are ready, process them in the format used by Carrot:
Carrot::Async::parallelFor(meshletCount, [&](std::size_t index) {
auto& meshoptMeshlet = meshoptMeshlets[index];
auto& carrotMeshlet = primitive.meshlets[meshletOffset + index];
carrotMeshlet.vertexOffset = vertexOffset + meshoptMeshlet.vertex_offset;
carrotMeshlet.vertexCount = meshoptMeshlet.vertex_count;
carrotMeshlet.indexOffset = indexOffset + meshoptMeshlet.triangle_offset;
carrotMeshlet.indexCount = meshoptMeshlet.triangle_count*3;
}, 32);
}
And here’s how to use it after simplification:
for(const auto& group : groups) {
// ... merge meshlets ...
// ... simplify merge result ...
if(simplifiedIndexCount > 0) {
appendMeshlets(primitive, simplifiedIndexBuffer);
}
And that’s it!
I now have all the buildings blocks to generate a LOD hierarchy, let’s combine everything!
Merging everything together
Let’s go step-by-step:
Step 1: Initial clustering. I just need to build meshlets from the original index buffer:
static void generateClusterHierarchy(LoadedPrimitive& primitive) {
// level 0
// tell meshoptimizer to generate meshlets
auto& indexBuffer = primitive.indices;
std::size_t previousMeshletsStart = 0;
appendMeshlets(primitive, indexBuffer);
Then, I generate each LOD iteratively, based on the previous LOD. That is, LOD n+1 is generated from LOD n:
// level n+1
const int maxLOD = 25; // I put a hard limit, but 25 might already be too high for some models
for (int lod = 0; lod < maxLOD; ++lod) {
float tLod = lod / (float)maxLOD;
// find out the meshlets of the LOD n
std::span<Meshlet> previousLevelMeshlets = std::span { primitive.meshlets.data() + previousMeshletsStart, primitive.meshlets.size() - previousMeshletsStart };
if(previousLevelMeshlets.size() <= 1) {
return; // we have reached the end
}
Step 2: groups meshlets.
std::vector<MeshletGroup> groups = groupMeshlets(primitive, previousLevelMeshlets);
Step 3: simplify merged results
// ===== Simplify groups
const std::size_t newMeshletStart = primitive.meshlets.size();
for(const auto& group : groups) {
// meshlets vector is modified during the loop
previousLevelMeshlets = std::span { primitive.meshlets.data() + previousMeshletsStart, primitive.meshlets.size() - previousMeshletsStart };
std::vector<unsigned int> groupVertexIndices;
// add cluster vertices to this group
for(const auto& meshletIndex : group.meshlets) {
const auto& meshlet = previousLevelMeshlets[meshletIndex];
std::size_t start = groupVertexIndices.size();
groupVertexIndices.resize(start + meshlet.indexCount);
for(std::size_t j = 0; j < meshlet.indexCount; j++) {
groupVertexIndices[j + start] = primitive.meshletVertexIndices[primitive.meshletIndices[meshlet.indexOffset + j] + meshlet.vertexOffset];
}
}
// simplify this group
const float threshold = 0.5f;
std::size_t targetIndexCount = groupVertexIndices.size() * threshold;
float targetError = 0.9f * tLod + 0.01f * (1-tLod);
unsigned int options = meshopt_SimplifyLockBorder; // we want all group borders to be locked (because they are shared between groups)
std::vector<unsigned int> simplifiedIndexBuffer;
simplifiedIndexBuffer.resize(groupVertexIndices.size());
float simplificationError = 0.f;
std::size_t simplifiedIndexCount = meshopt_simplify(simplifiedIndexBuffer.data(), // output
groupVertexIndices.data(), groupVertexIndices.size(), // index buffer
&primitive.vertices[0].pos.x, primitive.vertices.size(), sizeof(Carrot::Vertex), // vertex buffer
targetIndexCount, targetError, options, &simplificationError
);
simplifiedIndexBuffer.resize(simplifiedIndexCount);
I want to point out this line: float targetError = 0.9f * tLod + 0.01f * (1-tLod);. This allows high fidelity LODs to only be deformed by 1% during the simplification process, but low fidelity LODs can be deformed by up to 90%! This value is a bit high, I will reduce it further in the article when taking other points into consideration.
At this point, the goal is to allow the simplifier to reduce triangles as much as possible, even if it means getting an ugly mesh at the end. Remember, this ugly mesh should be only a few dozens pixels high/wide in the final render, so it does not have to be perfect.
Step 4: split simplification result:
// ===== Generate meshlets for this group
appendMeshlets(primitive, simplifiedIndexBuffer);
for(std::size_t i = newMeshletStart; i < primitive.meshlets.size(); i++) {
primitive.meshlets[i].lod = lod + 1;
}
}
Step 5: prepare for next iteration
previousMeshletsStart = newMeshletStart;
}
}
previousMeshletsStart is used to know the offset inside primitive.meshlets for the meshlets of LOD lod-1.
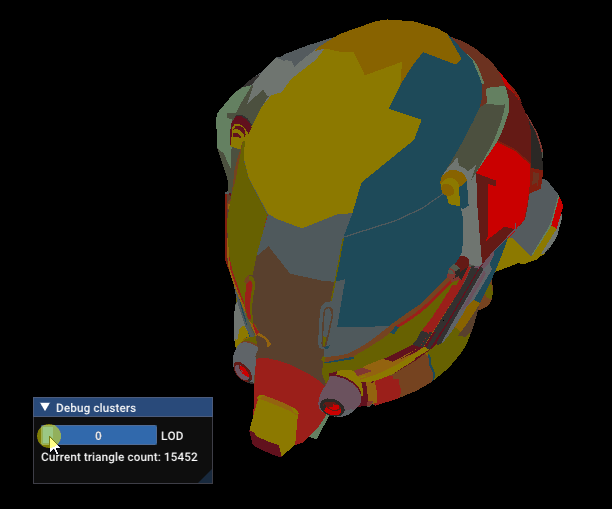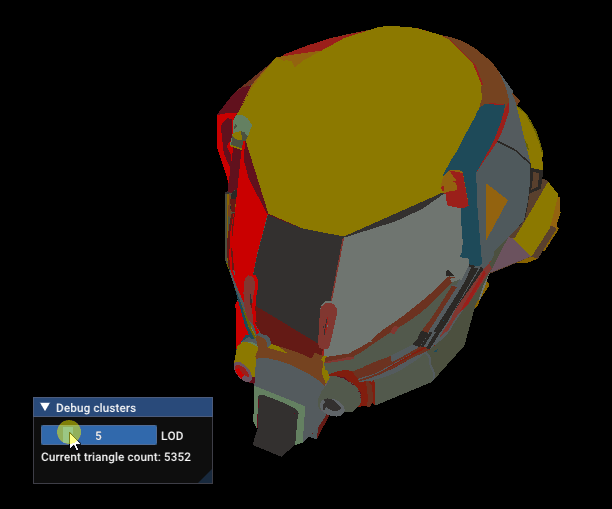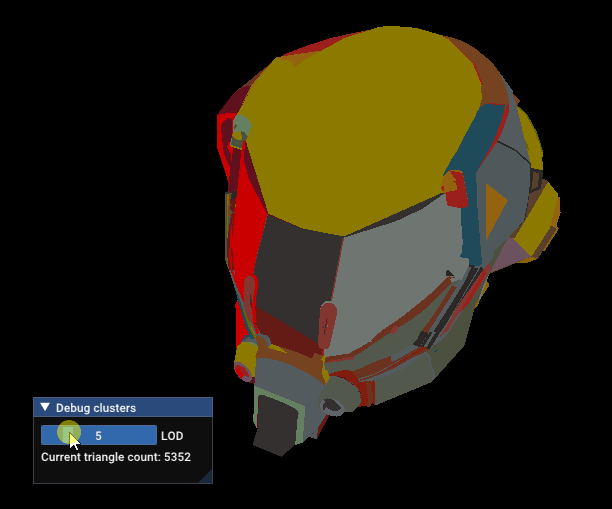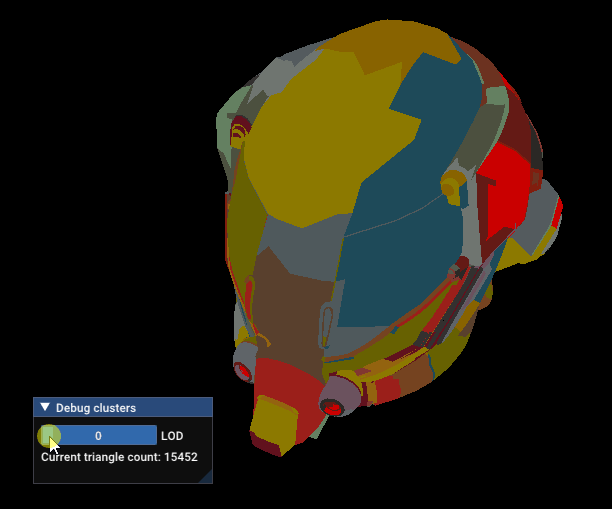
Here’s the result on the Standford bunny (with maxLOD = 10):
Standford bunny with different levels of simplification, each meshlet is represented by a different color.
Welding close enough vertices 1: the bruteforce approach
The implementation explained in the parts before this one works nicely for fully connected meshes, but it fails with faceted meshes:
Damaged Helmet simplification gets stuck
The reason is, the simplification process does not have enough connected triangles to match the requested simplification factor without creating too much error. This point is mentionned in meshoptimizer’s documentation:
For meshes with inconsistent topology or many seams, such as faceted meshes, it can result in simplifier getting “stuck” and not being able to simplify the mesh fully. Therefore it’s critical that identical vertices are “welded” together, that is, the input vertex buffer does not contain duplicates. Additionally, it may be possible to preprocess the index buffer (e.g. with meshopt_generateShadowIndexBuffer) to discard any vertex attributes that aren’t critical and can be rebuilt later.
Therefore, I decided to merge vertices that are close enough to push the simplifier to remove more triangles. To do so, I create a map that converts a vertex index to another vertex index, which will correspond to its closest neighbor. This closest neighbor might be the original vertex itself. Because there are as many vertices as entries in this map, allocating a vector works well and the index of an element will be the vertex index.
Let’s make a bruteforce and naive implementation of this, it will become clearer:
// initialize mapping
std::vector<std::int64_t> vertexRemap;
const std::size_t vertexCount = primitive.vertices.size();
vertexRemap.resize(vertexCount);
for(auto& v : vertexRemap) {
v = -1;
}
for(std::int64_t v = 0; v < vertexCount; v++) {
const Carrot::Vertex& currentVertex = primitive.vertices[v];
std::int64_t replacement = -1;
// due to the way we iterate, all indices starting from v will not be remapped yet
for(std::int64_t potentialReplacement = 0; potentialReplacement < v; potentialReplacement++) {
const Carrot::Vertex& otherVertex = primitive.vertices[vertexRemap[potentialReplacement]];
// TODO: if otherVertex is closer to currentVertex than 'replacement' is,
// then replacement will point to otherVertex
}
if(replacement == -1) {
vertexRemap[v] = v;
} else {
vertexRemap[v] = replacement;
}
}
return vertexRemap;
Obviously, iterating over most vertices to find the neighbor of a single vertex is very much not good™. I will get around to optimizing this in the next part.
For now I need a metric to know where a vertex is a better candidate for merging than another one.
First, I obviously want to merge only if the vertex is close enough in space:
// maxDistance is defined *somewhere*
float maxDistanceSq = maxDistance*maxDistance;
const Carrot::Vertex& currentVertex = primitive.vertices[v];
std::int64_t replacement = -1;
// due to the way we iterate, all indices starting from v will not be remapped yet
for(std::int64_t potentialReplacement = 0; potentialReplacement < v; potentialReplacement++) {
const Carrot::Vertex& otherVertex = primitive.vertices[vertexRemap[potentialReplacement]];
const float vertexDistanceSq = glm::distance2(currentVertex.pos, otherVertex.pos);
if(vertexDistanceSq <= maxDistanceSq) {
replacement = potentialReplacement;
}
}
glm::distance2 is the distance between two points, squared. This is cheaper to compute than computing the distance which requires a square root.
However, ignoring other information can lead to merging vertices which have very different attributes. I have decided to focus on UV coordinates, to avoid having unrelated parts of textures to be applied to an invalid part of the mesh:
// maxDistance and maxUVDistance are defined *somewhere*
float maxDistanceSq = maxDistance*maxDistance;
float maxUVDistanceSq = maxUVDistance*maxUVDistance;
const Carrot::Vertex& currentVertex = primitive.vertices[v];
std::int64_t replacement = -1;
// due to the way we iterate, all indices starting from v will not be remapped yet
for(std::int64_t potentialReplacement = 0; potentialReplacement < v; potentialReplacement++) {
const Carrot::Vertex& otherVertex = primitive.vertices[vertexRemap[potentialReplacement]];
const float vertexDistanceSq = glm::distance2(currentVertex.pos, otherVertex.pos);
if(vertexDistanceSq <= maxDistanceSq) {
const float uvDistanceSq = glm::distance2(currentVertex.uv, otherVertex.uv);
if(uvDistanceSq <= maxUVDistanceSq) {
replacement = potentialReplacement;
maxDistanceSq = vertexDistanceSq;
maxUVDistanceSq = uvDistanceSq;
}
}
}
Put all this code into a function like std::vector<std::int64_t> mergeByDistance(const LoadedPrimitive& primitive, float maxDistance, float maxUVDistance), and you have a way to simplify your mesh further!
Remains the question of how to use this vertexRemap vector.
To apply the vertex remap, the basic idea is simple: everywhere a vertex is accessed by its index inside the vertex buffer, add an indirection through the vertex remap:
vertices[myIndex] would transform into vertices[vertexRemap[myIndex]].
Therefore, there are two spots where this needs to be done:
groupMeshlets:auto getVertexIndex = [&](std::size_t index) { - return primitive.meshletVertexIndices[primitive.meshletIndices[index + meshlet.indexOffset] + meshlet.vertexOffset]; + std::size_t vertexIndex = primitive.meshletVertexIndices[primitive.meshletIndices[index + meshlet.indexOffset] + meshlet.vertexOffset]; + return static_cast<std::size_t>(vertexRemap[vertexIndex]); };- Merging clusters:
// add cluster vertices to this group for(const auto& meshletIndex : group.meshlets) { const auto& meshlet = previousLevelMeshlets[meshletIndex]; std::size_t start = groupVertexIndices.size(); groupVertexIndices.resize(start + meshlet.indexCount); for(std::size_t j = 0; j < meshlet.indexCount; j++) { - groupVertexIndices[j + start] = primitive.meshletVertexIndices[primitive.meshletIndices[meshlet.indexOffset + j] + meshlet.vertexOffset]; + groupVertexIndices[j + start] = vertexRemap[primitive.meshletVertexIndices[primitive.meshletIndices[meshlet.indexOffset + j] + meshlet.vertexOffset]]; } }
Last thing to do is to determine maxDistance and maxUVDistance for the mergeByDistance call. This requires a lot of fine-tuning based on your models and here’s what I have decided on at the time of writing:
const float maxDistance = (tLod * 0.1f + (1-tLod) * 0.01f) * simplifyScale;
const float maxUVDistance = tLod * 0.5f + (1-tLod) * 1.0f / 256.0f;
simplifyScaleis the size of the object, which can be queried viameshopt_simplifyScale.- High detail LODs should merge vertices which are less than 1% apart (relative to the size of the object), and whose UVs are a maximum of 1 pixel apart (for a 256x256 texture).
- Low detail LODs should merge vertices which are less than 10% apart (relative to the size of the object), and whose UVs are a maximum of half the texture apart.
Welding close enough vertices 2: k-d trees
The major point to improve in the previous chapter of this article is performance: I need a way to merge vertices by distance, without iterating over each vertex.
That is, for a given vertex, I need to find the neighboring vertices that are less than maxDistance units away, without having to look through all vertices.
For this problem, I decided to use k-d trees: a binary space partionning data structure. This article is already long and I don’t know enough about k-d trees to discuss them in details so I will focus on what I needed to do to use them.
You can see the implementation here, but it is not properly tested so there might be surprises hiding in this code.
⚠️ Update: This implementation has a major flaw, see the follow-up article.
I advise to build a k-d tree per LOD, with the vertices of the previous LOD. Building a single k-d tree for the entire mesh has the following issues:
- There is no guarantee vertices are stable between LODs: I think nothing prevents a vertex to simplify to a vertex that was not inside one of the previously simplified versions of the original mesh.
- I wanted to merge vertices that are close enough in the current simplified mesh, and reduce vertex count. By restricting the k-d tree to vertices inside the previous LOD, I can ensure that at best I do simplify the mesh further, and at worst I don’t modify the mesh.
Then it becomes a “simple” case of finding the neighbors of a vertex and picking the closest in both space and UV coordinates (and any other attributes you want to use). With 3D positions and UV coordinates, you can represent the mesh inside a 5D tree, with XYZ and UV as the 5 coordinates. My implementation only supports 3 dimensions and I check UV are querying for spatial information, but it should be trivial to expand it to more dimensions.
Here’s the result on the Damaged Helmet glTF sample, with a maximum distance of 50%:
Damaged Helmet LODs with maxDistance = 0.5 for the lowest LOD.
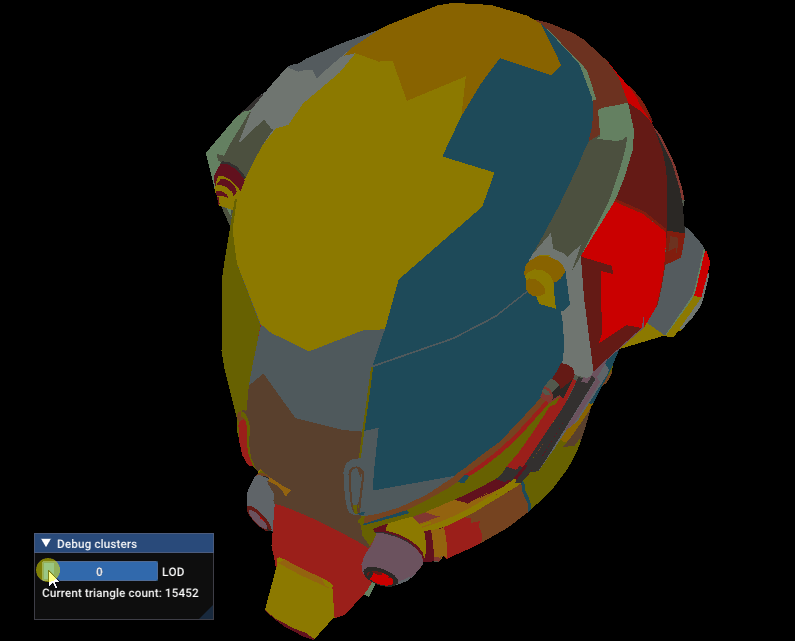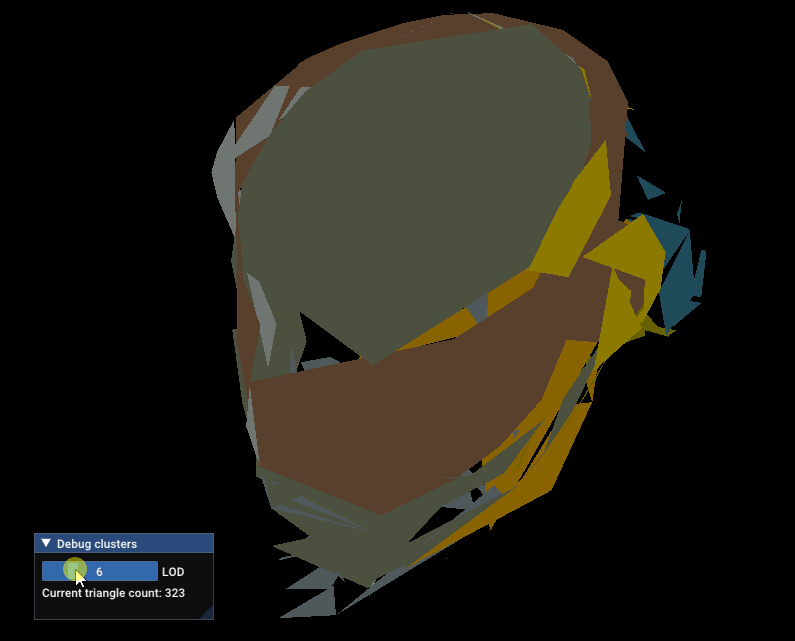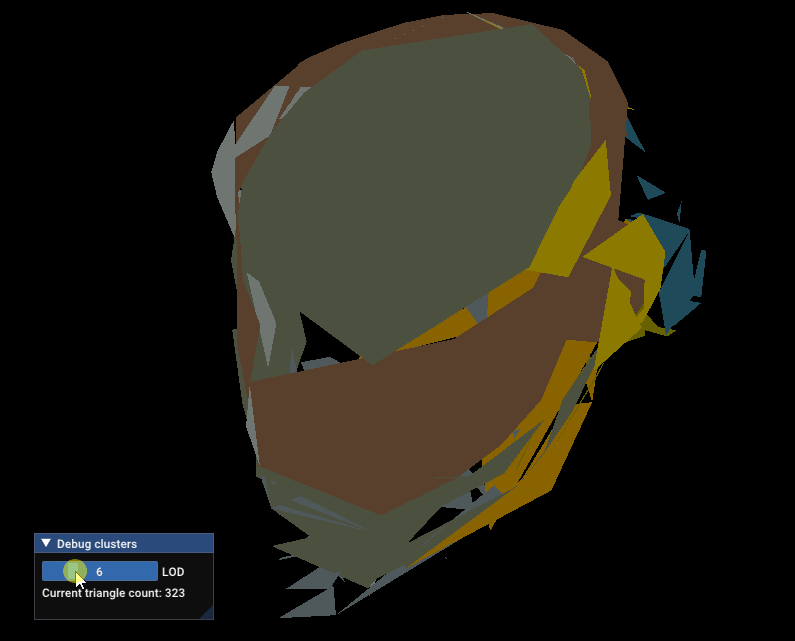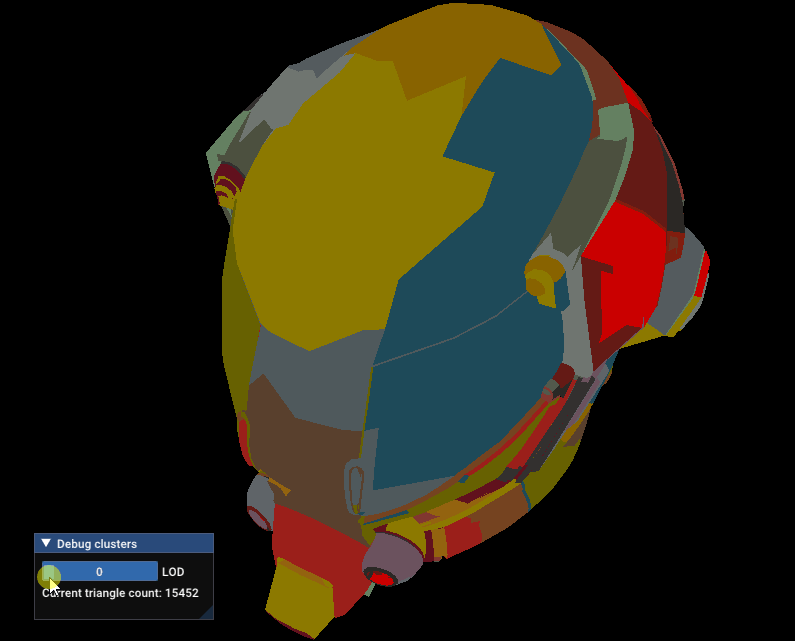
50% of the size of the mesh is a bit too big, let’s reduce it to 10%
Damaged Helmet LODs with maxDistance = 0.1 for the lowest LOD.
Not perfect, but that’s much better!
Current bugs & tuning
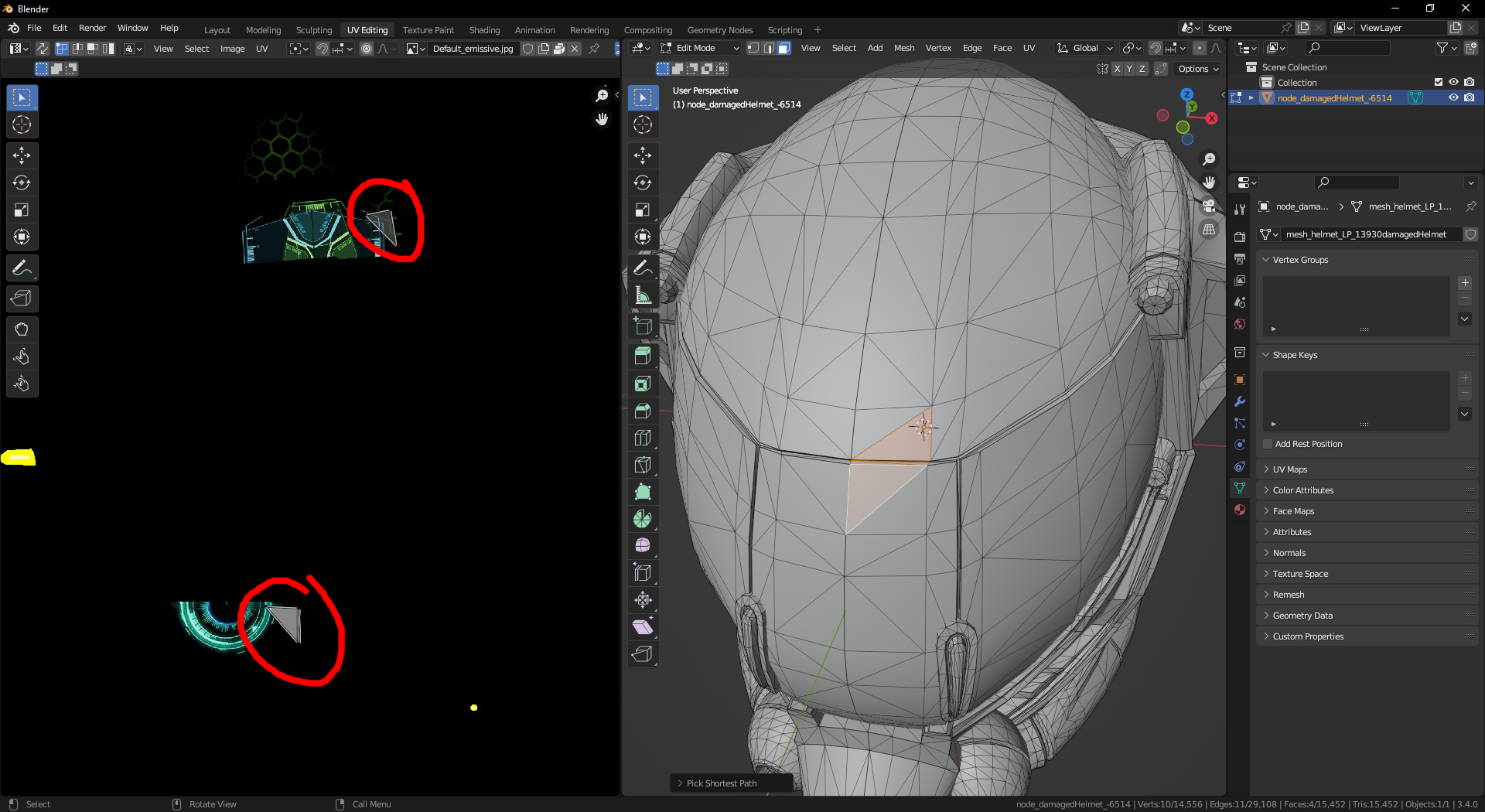
You probably noticed in the previous image that the DamagedHelmet has a lot of holes in its lowest detailed LODs. My current method for welding vertices seems to struggle a lot with faceted meshes (like the DamagedHelmet). This is due to the difference in UVs being too great for the welding process to merge some faces of the borders of the visor.
This can be seen inside Blender: by importing the model, selecting the UV edition view, and selecting a few triangles which never connect inside my implementation; you can clearly see that the faces have UVs coordinates which differ a lot:
DamagedHelmet opened in Blender, UV edition view opened. Two spatially-close faces are selected and very far apart in UV space.
However, the reason why I check UVs is this:
DamagedHelmet simplified with no respect to UVs, texture gets scrambled as random faces of the model get non-matching UVs.
Completely ignoring UVs when welding produces this atrocity! This is because some vertices are spatially close, but their UV coordinates are not close at all.
Unreal Engine seems to have no issue with this model (tested in UE5.3), so I will have to continue looking for ideas to merge spatially close vertices. I will have to check whether ignoring the normal was a good idea or not.
Finding thresholds that “look good” is a bit difficult with this current implementation. However, I believe I have found some reasonable values for now. One needs to remember that the lowest LOD are expected to be seen from far away, so trading visual fidelity for lower triangle counts can be worth it; as long as no one notices.
Next steps
So what is next for this series?
-
Automatic LOD selection. Currently LODs are manually selected, but the next step is to select the proper LOD based on the screensize of the object.
-
Improvements on simplification quality. As demonstrated with the DamagedHelmet sample, the simplification is not very satisfying and can be improved.
-
Performance (will likely be a post all of its own). Building the LOD cluster can take a while with big models, and rendering these clusters also takes a while.
ℹ️ A new article is out! It explains everything I have done to improve on this article’s LOD generation. You should check it out!