Recreating Nanite: LOD generation - faster, better, simpler
Table of contents:
⚠️ This article is a short follow up on Recreating Nanite: LOD generation. You should read it before reading this article!
Introduction
In the state at the end of the previous article on LOD generation, there were a few issues:
- Some meshes got basically destroyed by the simplification.
- Facet-ed meshes developed gaps between facets, which widened with each further LOD.
- Performance: I tried to generate LODs for the Happy Buddha model, and it took a bit more than 4 minutes!
I am going to explain how I fixed these issues in this (short) article.
Fixing performance
Law of large numbers
The most optimal k-d trees are those which are balanced. This means each node splits its children into two groups of equal size.
This way, querying for the closest neighbor of a point is at most O(log(n)).
However, balanced k-d trees require finding the median point of a set multiple times. One approach is to sort all points of the set, and take the middle value:
Vector<TElement> allElements; // list of elements, and TElement has a 'getPosition' method
Vector<std::size_t> setOfPointIndices; // indices of elements inside 'allElements'
Vector<std::size_t> points { stackAllocator };
points.setCapacity(setOfPointIndices.size());
for(std::size_t pointIndex : setOfPointIndices) {
points.pushBack(pointIndex);
}
points.sort([&](const std::size_t& a, const std::size_t& b) {
const float posA = allElements[a].getPosition()[axisIndex];
const float posB = allElements[b].getPosition()[axisIndex];
return posA < posB;
});
// vvv Find median after sorting vvv
pDestination->elementIndex = points[points.size() / 2];
pDestination->medianPoint = allElements[pDestination->elementIndex].getPosition();
However, this method is obviously going to get worse and worse when the amount of points increases. In the case of LOD generation, the points are vertices of the mesh. So more detailed meshes will perform worse and worse.
What if there was a way to approximate the result without iterating over all these points?
Turns out there is, if you are willing to make some assumptions about the input data. If the positions of vertices are normally distributed or uniformly distributed, then the average is the same as the median. Alternatively, you can also choose to assume the positions are normally distributed and not care about whether it is true, that’s the choice I took.
In probability theory, the law of large numbers (LLN) is a mathematical theorem that states that the average of the results obtained from a large number of independent and identical random samples converges to the true value, if it exists.
In other words, take some random values from your set, average them, and you will get close to the real average. That’s the basis for Monte Carlo methods.
Let’s do this:
Vector<TElement> allElements; // list of elements, and TElement has a 'getPosition' method
Vector<std::size_t> setOfPointIndices; // indices of elements inside 'allElements'
Vector<std::size_t> points { tempAllocator };
// make sure there are enough values to have a meaningful average
if(subset.size() < 512) {
points.setCapacity(setOfPointIndices.size());
for(std::size_t pointIndex : setOfPointIndices) {
points.pushBack(pointIndex);
}
} else {
// randomly select 512 samples
// then these samples will get sorted below
points.resize(512);
for(std::size_t i = 0; i < 512; i++) {
std::size_t randomIndex = Carrot::RNG::randomFloat(0.0f, setOfPointIndices.size()-1);
points[i] = setOfPointIndices[randomIndex];
}
}
points.sort([&](const std::size_t& a, const std::size_t& b) {
const float posA = allElements[a].getPosition()[axisIndex];
const float posB = allElements[b].getPosition()[axisIndex];
return posA < posB;
});
pDestination->elementIndex = points[points.size() / 2];
pDestination->medianPoint = allElements[pDestination->elementIndex].getPosition();
I am no probability genius, this technique is suggested in the Wikipedia article on k-d trees.
Doing less work
Meshoptimizer simplification accounted for most of the runtime of my algorithm. The whole point is simplification, so this may seem normal, but there is something that can be done to speed things up.
Meshoptimizer’s simplification starts by iterating over all vertices of the vertex buffer, even if they are not used inside the index buffer. This means that we can reduce the time spent by meshoptimizer by creating a small vertex buffer just for simplification!
ℹ️ Meshoptimizer’s author has plans to fix this issue in the future: Meshlets Merging and Simplification discussion on GitHub
Instead of providing the index buffer created from grouped meshlets to Meshoptimizer, the idea is:
- Remap vertices used by the grouped meshlets into a new vertex buffer
- Remap indices used by the grouped meshlets to point to the new vertex buffer
- Simplify via Meshoptimizer, using this new index buffer
- Remap indices back to an index inside the index buffer used for the entire mesh
You can see the code difference right here!
This single optimization massively reduced the time to generate LODs on my machine.
However there are a few additional optimisations that can be done to reduce the workload:
- Remove duplicate edges and meshlet connections. This leads to faster partitioning. In pratice, this means “just” using a map or a set to determine which edges are present inside a meshlet. I used vectors before, and that was a mistake.
- Remove degenerate triangles for simplification. After meshlet grouping, but before simplification, I merge vertices that are “close enough” with the k-d trees mentionned earlier in this article. However, this means some triangles will collapse to a single point. In this case, there is no point in trying to simplify them, so I just ignore them when creating the index buffer for the grouped meshlets.
- Find out vertex neighbors in parallel. Instead of sequentially finding vertex neighbors to determine which ones are “close enough”, this can be done in parallel. This can have a huge memory requirement if you are not careful, but it is much much faster.
All 3 points (and more!) were implemented in this commit.
Fixing quality
Finally, the last step is to improve quality.
The algorithm explained in the previous article has a major flaw in it: I spent a lot of time explaining that borders between clusters must match to avoid seams between different LODs.
And then I simplify said borders of clusters by merging vertices with their closest neighbor…
Therefore:
- facet-ed meshes have gaps which get bigger with each LOD iteration
- high-poly meshes have extremely ugly LODs because they get simplified too much
- seams appear between clusters of different LODs.
Thefore, the fix is to determine which edges are part of the cluster boundary, and not modifying these edges at all. The first step is to find which edges are part of the boundary. This is very similar to determining which meshlets are connected: boundary edges are edges which are not shared between meshlets:
/**
* Connections betweens meshlets
*/
struct MeshletEdge {
explicit MeshletEdge(std::size_t a, std::size_t b): first(std::min(a, b)), second(std::max(a, b)) {}
bool operator==(const MeshletEdge& other) const = default;
const std::size_t first;
const std::size_t second;
};
struct MeshletEdgeHasher {
std::size_t operator()(const MeshletEdge& edge) const {
std::size_t h = edge.first;
Carrot::hash_combine(h, edge.second);
return h;
}
};
/**
* Find which vertices are part of meshlet boundaries. These should not be merged to avoid cracks between LOD levels
*/
static Carrot::Vector<bool> findBoundaryVertices(Carrot::Allocator& allocator, LoadedPrimitive& primitive, std::span<Meshlet> meshlets) {
Carrot::Vector<bool> boundaryVertices { allocator };
boundaryVertices.resize(primitive.vertices.size());
boundaryVertices.fill(false);
// meshlets represented by their index into 'previousLevelMeshlets'
std::unordered_map<MeshletEdge, std::unordered_set<std::size_t>, MeshletEdgeHasher> edges2Meshlets;
// for each meshlet
for(std::size_t meshletIndex = 0; meshletIndex < meshlets.size(); meshletIndex++) {
const auto& meshlet = meshlets[meshletIndex];
auto getVertexIndex = [&](std::size_t index) {
const std::size_t vertexIndex = primitive.meshletVertexIndices[primitive.meshletIndices[index + meshlet.indexOffset] + meshlet.vertexOffset];
return vertexIndex;
};
const std::size_t triangleCount = meshlet.indexCount / 3;
// for each triangle of the meshlet
for(std::size_t triangleIndex = 0; triangleIndex < triangleCount; triangleIndex++) {
// for each edge of the triangle
for(std::size_t i = 0; i < 3; i++) {
MeshletEdge edge { getVertexIndex(i + triangleIndex * 3), getVertexIndex(((i+1) % 3) + triangleIndex * 3) };
if(edge.first != edge.second) {
edges2Meshlets[edge].insert(meshletIndex);
}
}
}
}
for(const auto& [edge, meshlets] : edges2Meshlets) {
if(meshlets.size() == 1) {
boundaryVertices[edge.first] = true;
boundaryVertices[edge.second] = true;
}
}
return boundaryVertices;
}
Then, remains an easy check whether a vertex is on a boundary when merging with neighbors: if the vertex is on a boundary, do not merge with neighbors.
As usual, the implementation is available here: Click me! and click me too! (The logic was inverted…)
Conclusion
Those fixes massively improved the quality and performance of my LOD generation! As written in the introduction, the Happy Buddha model took 4min to simplify on my Ryzen 7 2700X, and now it takes “only” 40s! Also, LODs actually resemble the original model.
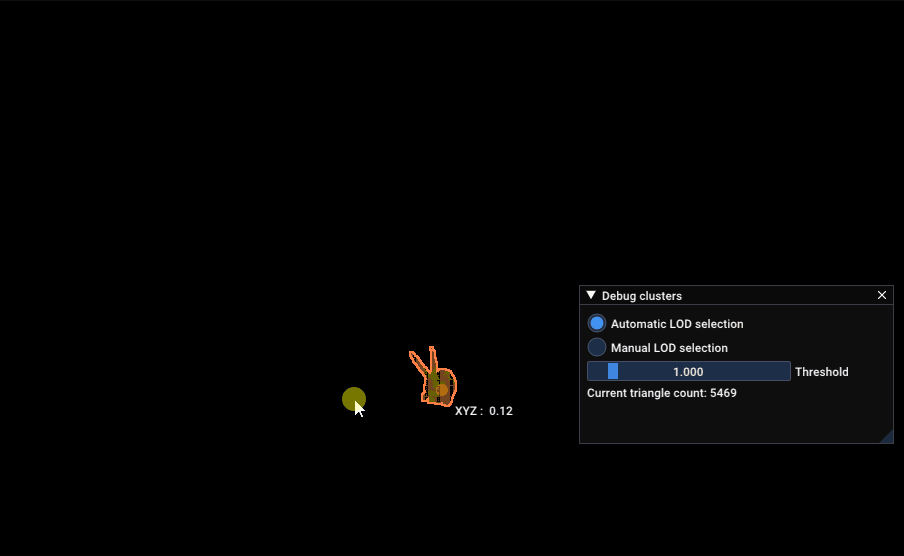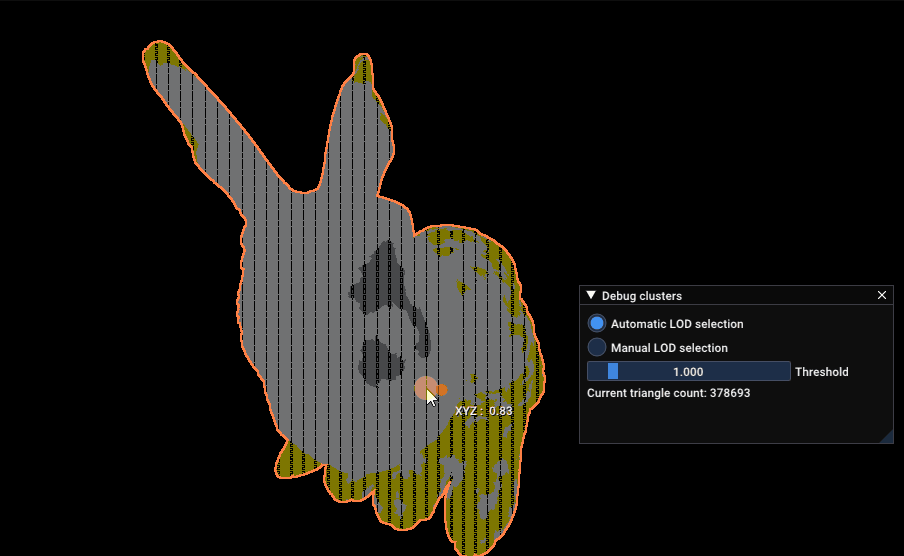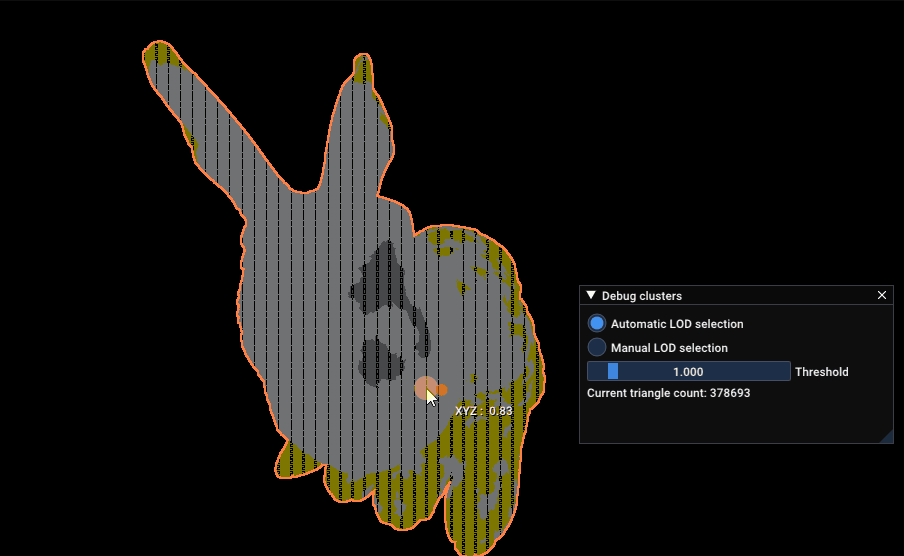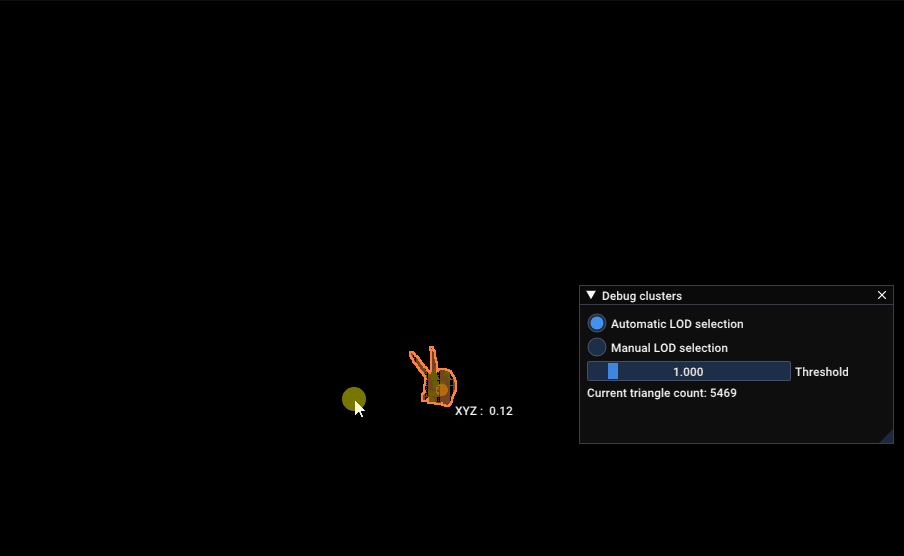
Finally, I’ll leave you with this GIF of the not a standford bunny model by Jocelyn Da Prato automatically selecting its LOD, per cluster, in real time:
not a standford bunny model automatically selecting LOD levels, per cluster, depending on the screen size of each cluster. Numbers on each clusters represent the current LOD for the rendered cluster.