Recreating Nanite: Runtime LOD selection
This article is part of the “Recreating Nanite” series, you should read the previous articles to fully understand what is going on here!
Table of contents:
Related commits:
- Runtime selection of LODs v1
- Fix error projection not using camera position properly
- Fixing cluster bound generation
Theory
As explained in the previous articles, I now have a hierarchy of clusters with LODs. But now the culmination of these articles is to actually select the LODs at runtime: we want to render the best mesh possible for a given size on screen.
However, contrary to the rest of the Nanite tech, the presentation pdf is a bit vague about the metrics used to switch between LODs. Of course Epic may want to keep some secrets, but anyone who would want to use virtual geometry will need to come up with a metric to select LODs. What I know, is that I want to select LODs if they are detailed enough: I want the lowest detailed mesh that still avoids less than 1 pixel error when compared to the original mesh, for its current screen size. The goal is to have a mesh that is perceptually the same as the original mesh when rendered at a given screen size.
How did I do it then?
When simplifying meshes, meshoptimizer outputs a simplification error. This is a float that represents the error, in terms of mesh extents, of the simplification.
I don’t know the algorithm behind it, so I am not 100% sure I understand the exact meaning of what this represents. I understand this simplification error as how much the shape of the mesh has been modified, as in how much smaller/bigger the mesh got in terms of its size. Of course not all parts of the mesh may shrink/grow that much so the actual bounding sphere may not change, but some parts may have “shrinked” by at most simplification error percents.
Displacement error represented between original mesh (circle) and simplified mesh (square)
By multiplying the simplification error by the size of the original mesh, you can get an error in world units that is no longer dependent on the mesh bounds.
However, because LOD generation is iterative, this simplification error is on-top of the simplification error due to the previous LOD. This mean that the simplification error cannot be used directly: one needs to accumulate error.
Here’s the outline of the algorithm when simplifying a meshlet group:
- Simplify the meshlet group, you will get the simplification error as a side output.
- Compute the bounds of the simplified group.
- Multiply the simplification error by the radius of the group. I will call this error
meshSpaceError. - Compute the maximum error of the child meshlets, and add it to
meshSpaceError. - Set the parent error and parent bounds of the meshlets from the previous-LOD group to
meshSpaceErrorand the bounds of the simplified mesh.
Note: meshlets of the same group must have the same error and bounds to make the same LOD decision. If you store per-meshlet bounds, you will get artefacts: expect missing meshlets, or overlapping meshlets!
Why add the maximum error of child meshlets? (Step 4)
If a parent is not simplified much, its error will be small, therefore its error may be less than its children’s errors, so the resulting error for the parent will be equal to the children’s errors. And clusters with parentError == selfError will never be rendered (explanation further down).
Additionally, error must increase when increasing LOD: LODs with fewer details have more simplification errors, because they are simplified more.
Furthermore, simplification is done iteratively, so the error of the parent is relative to the children. The error stored inside the meshlets must be somewhat “global”, ie the error of a parent must no longer depend from the child.
To solve this issue, I personally add the child errors to the parent’s error to make it increase. Not sure if that’s the correct way to do it, but works fine for me. This addition matches all that is required for the LOD system to work:
- Monotonically increasing error values
- Error values that are independent from other meshlets, which allows parallel selection of LODs!
Implementation
Let’s start by adding the necessary data to Meshlet:
struct Meshlet {
std::uint32_t vertexOffset = 0;
std::uint32_t vertexCount = 0;
std::uint32_t indexOffset = 0;
std::uint32_t indexCount = 0;
std::uint32_t lod = 0;
+ Math::Sphere boundingSphere;
+ Math::Sphere parentBoundingSphere;
+
+ // Meshlets form a graph where the root is the most simplified version of the entire model, and each node's children
+ // are the meshlets which were simplified to create that node.
+ // Everything is expressed in mesh space here
+ float parentError = std::numeric_limits<float>::infinity(); // set to infinity if there is no parent (ie the node has no further simplification)
+ float clusterError = 0.0f;
};
For each meshlet, I store the group bounding sphere, the parent bounding sphere, as well as the error values for the group and the parent. These values will be shared by all meshlets of a same group. It is possible to reduce the memory footprint by adding an indirection and storing these values per group instead of per meshlet, but I decided to keep it simple for now.
The changes in Meshlet have to be replicated inside Cluster:
struct Cluster {
vk::DeviceAddress vertexBufferAddress = (vk::DeviceAddress)-1;
vk::DeviceAddress indexBufferAddress = (vk::DeviceAddress)-1;
std::uint8_t triangleCount;
std::uint32_t lod;
glm::mat4 transform{ 1.0f };
+ Math::Sphere boundingSphere{0.0f}; // xyz + radius (vec4)
+ Math::Sphere parentBoundingSphere{0.0f}; // xyz + radius (vec4)
+ float error = 0.0f;
+ float parentError = std::numeric_limits<float>::infinity();
};
This will make it available for shaders. The values are simply copied from meshlets when generating the clusters:
for(std::size_t i = 0; i < desc.meshlets.size(); i++) {
auto& cluster = gpuClusters[i + firstClusterIndex];
cluster.vertexBufferAddress = vertexData.view.getDeviceAddress() + vertexOffset;
cluster.indexBufferAddress = indexData.view.getDeviceAddress() + indexOffset;
const auto& meshlet = desc.meshlets[i];
+ cluster.boundingSphere = meshlet.boundingSphere;
+ cluster.parentBoundingSphere = meshlet.parentBoundingSphere;
+ cluster.parentError = meshlet.parentError;
+ cluster.error = meshlet.clusterError;
vertexOffset += sizeof(Carrot::Vertex) * meshlet.vertexCount;
indexOffset += sizeof(std::uint32_t) * meshlet.indexCount;
}
Writing errors to meshlets
LOD 0 clusters have no error and infinite parent error: you cannot get a more detailed model than the original one by simplification.
- appendMeshlets(primitive, indexBuffer);
+ {
+ Carrot::Vector<unsigned int> lod0Indices;
+ lod0Indices.resize(indexBuffer.size());
+ meshopt_Bounds lod0Bounds = meshopt_computeClusterBounds(
+ lod0Indices.data(), lod0Indices.size(),
+ &primitive.vertices[0].pos.x, primitive.vertices.size(), sizeof(Carrot::Vertex));
+ appendMeshlets(primitive, indexBuffer,
+ lod0Bounds, // boundingSphere
+ 0.0f // cluster error
+ );
+ }
Then after simplifying a group of meshlets:
// previousLevelMeshlets are meshlets from the LOD before the one being generated
// group.meshlets is the list of meshlets of the current group
// simplifiedIndexBuffer is the index buffer for the simplified mesh
// see previous articles on LOD generation for more information
// 1. compute group bounds from group mesh data
glm::vec3 min { +INFINITY, +INFINITY, +INFINITY };
glm::vec3 max { -INFINITY, -INFINITY, -INFINITY };
// remap simplified index buffer to mesh-wide vertex indices
for(auto& index : simplifiedIndexBuffer) {
index = group2meshVertexRemap[index];
const glm::vec3 vertexPos = glm::vec3 { primitive.vertices[index].pos.xyz };
min = glm::min(min, vertexPos);
max = glm::max(max, vertexPos);
}
Carrot::Math::Sphere simplifiedClusterBounds;
simplifiedClusterBounds.loadFromAABB(min, max);
// 2. compute group scale from group mesh data
float localScale = meshopt_simplifyScale(&groupVertexBuffer[0].pos.x, groupVertexBuffer.size(), sizeof(Carrot::Vertex));
meshoptimizer’s simplification routines return an error which is relative to the object, so we need to multiply by the object size to have a value in world units. This is necessary to have error values which are independent from one meshlet to the next.
// 3. multiply simplification error by size of group
// that way, simplification error is in world units instead of being relative to the mesh
float meshSpaceError = simplificationError * localScale;
float childrenError = 0.0f;
// 4. find max of child error (see Theory part of article for explanation)
for(const auto& meshletIndex : group.meshlets) {
const auto& previousMeshlet = previousLevelMeshlets[meshletIndex];
// ensure parent(this) error >= child(members of group) error
childrenError = std::max(childrenError, previousMeshlet.clusterError);
}
// 5. set parent errors of meshlets used to generate this LOD
meshSpaceError += childrenError;
for(const auto& meshletIndex : group.meshlets) {
previousLevelMeshlets[meshletIndex].parentError = meshSpaceError;
previousLevelMeshlets[meshletIndex].parentBoundingSphere = simplifiedClusterBounds;
}
// ...
appendMeshlets(primitive, simplifiedIndexBuffer,
simplifiedClusterBounds, // use same group bounds for all meshlets
meshSpaceError // use same error for all meshlets
);
After this, meshlets contain all the data necessary for culling!
Culling at runtime
Nanite has a fancy system to iterate over the entire graph of clusters. I decided to keep things simple for now: a flat list of all loaded clusters, and I will iterate over them all each frame. Is it performant? Probably not. Is it easy to understand? Absolutely!
Here’s what the render loop looks like before adding automatic LOD selection (details are not important):
// setting up state, see previous articles
// ...
for(const auto& [index, pInstance] : models) { // for each model rendered via virtual geometry
if(const auto instance = pInstance.lock()) {
if(!instance->enabled) {
continue;
}
if(instance->pViewport != renderContext.pViewport) {
continue;
}
packet.clearPerDrawData();
packet.unindexedDrawCommands.clear();
packet.useInstance(instance->instanceData);
std::uint32_t instanceIndex = 0;
for(const auto& pTemplate : instance->templates) {
std::size_t clusterOffset = 0;
for(const auto& cluster : pTemplate->clusters) {
// =========================
// Test whether we should render a given cluster. This is what I will focus on:
// =========================
if(testLOD(cluster, *instance)) {
auto& drawCommand = packet.unindexedDrawCommands.emplace_back();
drawCommand.instanceCount = 1;
drawCommand.firstInstance = 0;
drawCommand.firstVertex = 0;
drawCommand.vertexCount = std::uint32_t(cluster.triangleCount)*3;
triangleCount += cluster.triangleCount;
GBufferDrawData drawData;
drawData.materialIndex = 0;
drawData.uuid0 = instance->firstInstance + instanceIndex;
packet.addPerDrawData(std::span{ &drawData, 1 });
}
instanceIndex++;
clusterOffset++;
}
}
verify(instanceIndex == instance->instanceCount, "instanceIndex == instance->instanceCount");
if(packet.unindexedDrawCommands.size() > 0)
renderer.render(packet);
}
}
The part that really interest me for this article is the testLOD lamba used to know whether I want to render a cluster.
At this point, it is simply a check of Cluster::lod against a static int to show only clusters with the wanted LOD.
Let’s add automatic LOD selection!
The idea is:
- Transform a sphere S1 with its center at the center of the cluster
boundingSphere, and radiuserror, into view space. - Compute the radius in pixels of sphere S1 when rendered on screen, which will be named
clusterError. - Do the same for S2 with center
parentBoundingSphereand radiusparentError, store the result inparentError. - Finally, one can decide whether the cluster should be rendered: the cluster is rendered if
clusterError <= errorThreshold && parentError > errorThreshold.
What is errorThreshold?
This represents the maximum tolerated error, in pixels, of a cluster. I set it to 1 by default, to allow a maximum of 1 pixel difference between the original mesh and the selected LOD, at the current screen size.
Code time!
auto testLOD = [&](const Cluster& c, const ClusterModel& instance) {
if(lodSelectionMode == 0) {
return c.lod == globalLOD;
} else {
// assume a fixed fov and perspective projection
const float testFOV = glm::half_pi<float>();
const float cotHalfFov = 1.0f / glm::tan(testFOV / 2.0f);
const float testScreenHeight = renderContext.pViewport->getHeight();
// https://stackoverflow.com/questions/21648630/radius-of-projected-sphere-in-screen-space
auto projectErrorToScreen = [&](const Math::Sphere& sphere) {
if(!std::isfinite(sphere.radius)) {
return sphere.radius;
}
const float d2 = glm::dot(sphere.center, sphere.center);
const float r = sphere.radius;
return testScreenHeight / 2.0f * cotHalfFov * r / glm::sqrt(d2 - r*r);
};
// 1.
Math::Sphere projectedBounds {
c.boundingSphere.xyz,
std::max(c.error, 10e-10f)
};
const glm::mat4 completeProj = camera.getCurrentFrameViewMatrix() * instance.instanceData.transform * c.transform;
projectedBounds.transform(completeProj);
// 2.
const float clusterError = projectErrorToScreen(projectedBounds);
// 3.
Math::Sphere parentProjectedBounds {
c.parentBoundingSphere.xyz,
std::max(c.parentError, 10e-10f)
};
parentProjectedBounds.transform(completeProj);
const float parentError = projectErrorToScreen(parentProjectedBounds);
// 4.
return clusterError <= errorThreshold && parentError > errorThreshold;
}
};
Results and debug views
Here’s the result of all this work:
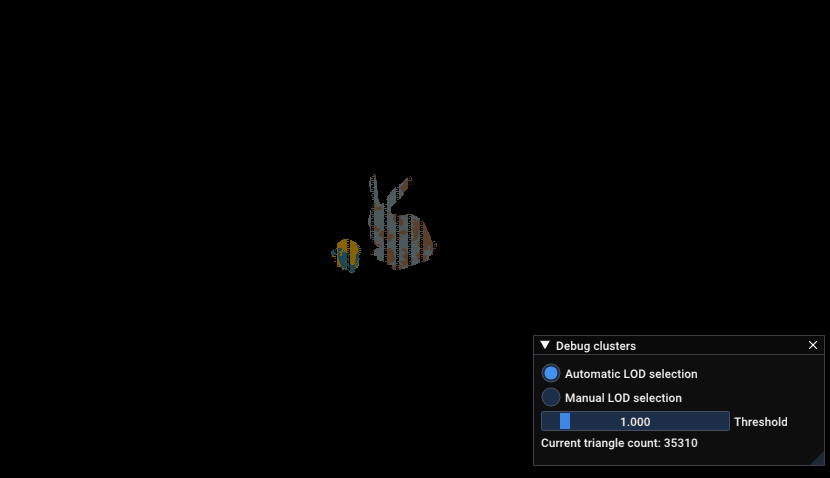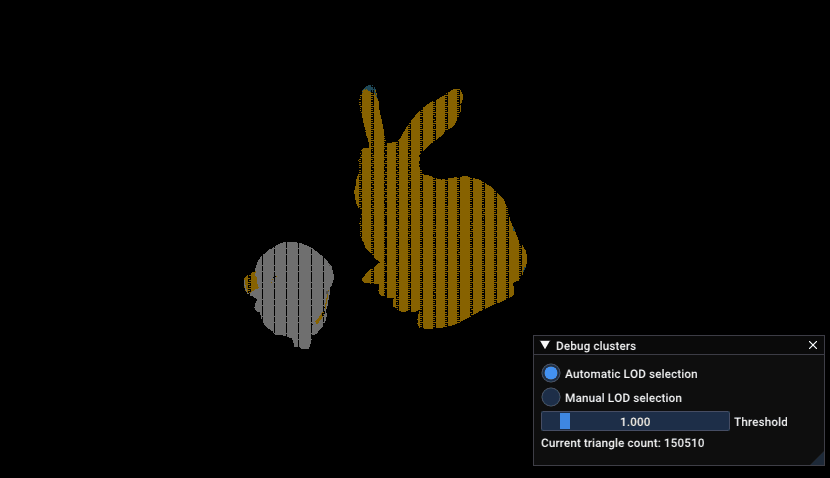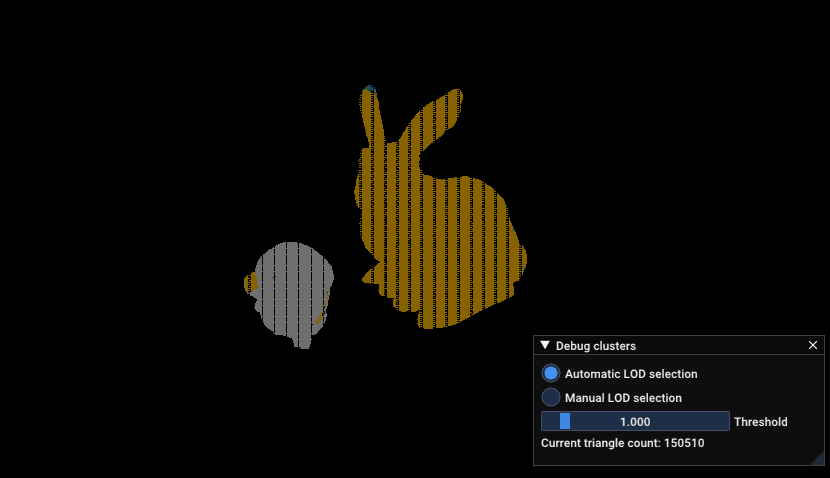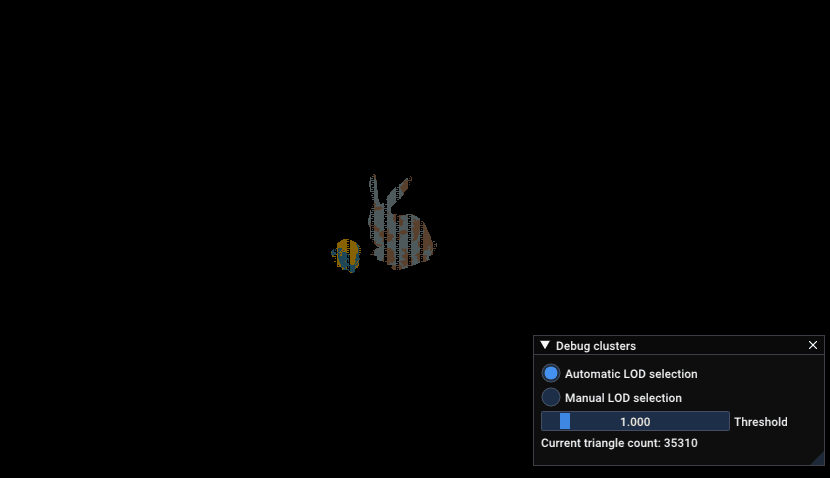
Zoom into DamagedHelmet and not a standford bunny, which shows the amount of triangle increasing when the camera gets near the models
If you want to go into recreating Nanite yourself too, you will want to have a few debug views!
I personally have:
- Triangle (different color per triangle)
- Cluster (different color per cluster)
- LOD (LOD index used to render a given pixel)
- Projected screen error (result of clusterError computed inside
testLOD) (error exaggerated by a factor of 10 for this screenshot)
Debug views with numbers are done with this shader: Smaller Numbers by P_Malin.
Here’s a similar zoom in than the previous GIF with the LOD view:
Zoom into DamagedHelmet and not a standford bunny, which shows the index of the LOD used to render parts of the model
Conclusion and special thanks
Finally, I have filled the main objective of a Nanite-like system: automatic LODs ! Of course, there are lots of features I want to add to the system, but this looks like a big milestone. For example, the LOD selection is done on the CPU, and it is done sequentially. This is not performant at all, so in the next article, I will explain how I replaced this CPU implementation with a mesh shader based LOD system!
Special thanks to JMS55 and LVSTRI from the Graphics Programming Discord, which through discussions, helped me find a somewhat clear way to explain the runtime selection.
The bunny model I used in this article is: not a standford bunny model by Jocelyn Da Prato.